5次元立方体に関する数学的解説
先日、以下のツイートがややバズりました。
VR界で4次元立方体がバズってるから私が作った5次元立方体ももうちょい流行ってもよくない? pic.twitter.com/unagNhuoqg
— Hibit (@hibit_at) 2018年9月6日
主にプログラミングに関する解説については、qiitaに載せましたが、
5次元のままでは3次元で描画できないので3次元に投影する必要があります。投影の方法としてはステレオ投影が有名ですが、これだけだと1次元しか集約できないので、その他に斜投影を使います。
の辺りは数学的な予備知識がないとサッパリだと思うので、このエントリではその辺りに解説を加えていきたいと思います。
そもそも次元とは
ここではn次元空間に限って話そうと思います。
- 1次元は軸が1つ → 直線
- 2次元は軸が2つ → 平面
- 3次元は軸が3つ → 空間
というのは比較的理解しやすいと思いますが、じゃあその次に来る4次元とは何なのか? というのは非常に想像しづらいと思います。まず言っておかなければならないのは、
「4次元空間 = 3次元空間 + 時間」ではない
ということです。確かに時間を加えると新たな情報の軸ができますが、それは空間と等価ではありません。あくまで擬似的な解釈です。更に5次元までいくと「5次元空間 = 3次元空間 + 時間 + 並行世界だ」という意見も見かけますが、それも間違い、というか不完全な解釈です。
2次元の場合に落として考えるとわかりやすいと思いますが、1m*1mの正方形が1秒間存在したら「2次元空間+時間」という意味では3次元ですが、これは「立方体」と言えるでしょうか。言えないです。そもそも1m = 1sではないですし、3次元空間ならばできるはずの回転といった動作が定義できません。同様に、立法体が1秒間存在したとしても、それをもって3次元生命体である我々が「4次元立方体(八胞体、Tesseract)を見た!」とは言えません。(相対性理論まで考えれば光速×時間は空間と等価になりミンコフスキー空間内での回転を考えることができますが、そういうのはおいといて)
5次元空間はあくまで5次元の空間です。我々が普段、「空間」として3つの軸が5つに増えただけです。ただ、我々がそれを観ることはどうしても不可能です。
感じることは出来ないが、考えることはできる
我々がありのままの多次元立方体を観るのは不可能です。あきらめましょう。
……というのでは悲しいので、なんとかして観る方法を考えます。
いきなり5次元だとハードルが高いので、4次元立方体から考えます。
 ↑こんなやつ
↑こんなやつ
ここでも次元を落として考えましょう。3次元の物体の形状をどうにかして相手に伝えたい時に、紙に描きます。3次元立方体を描くとしたら、次のような図を描くのではないでしょうか。(そして今わたしも2次元のディスプレイに写しています)

ここで我々は無意識に「投影(projection)」という行為を行っています。太陽の影が人間の体(3次元)を地面に影(2次元)として写すように、元の情報を「押しつぶして」次元を1つ下げているのです。では、どのように押しつぶすのか? 人間が立方体を紙に描くときは、上の図のように「いい感じの」角度で描きますが、これだと2次元人に立方体を説明するのは困難だと思います。多分、
「なんだこの歪んだ形は? これが正方形なんて信じられないよ」
と言われると思います。これが歪んでないと感じるのは、あなたが3次元人だからです。愚かな2次元人に説明しやすくするために、もう少し「真っ直ぐ」な位置に太陽を設定するとどうでしょう。
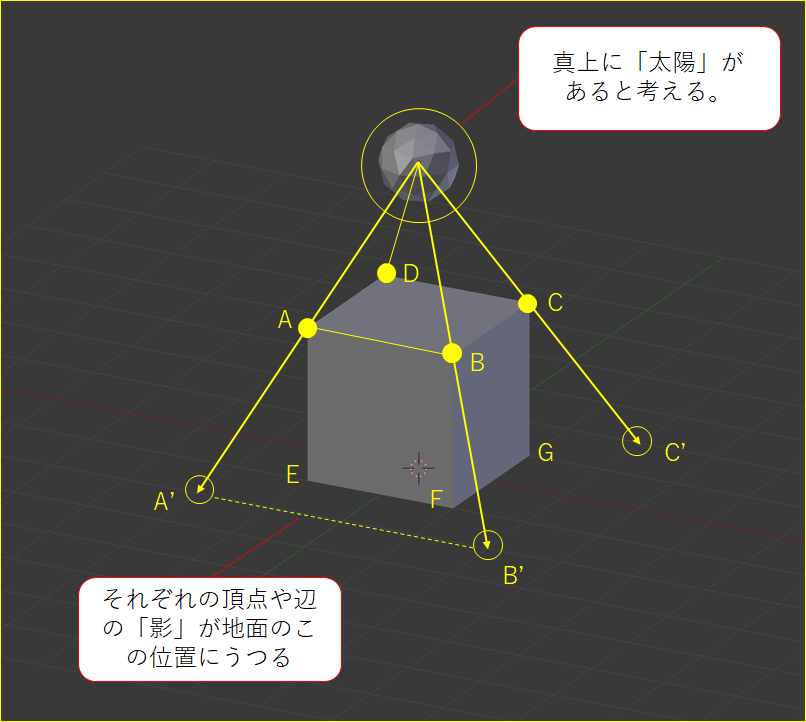
立方体の真上に太陽があるとします。ABCDの点は、A'B'C'D'の位置に影が落ちることがわかると思います。これを太陽の視点から見下ろすと
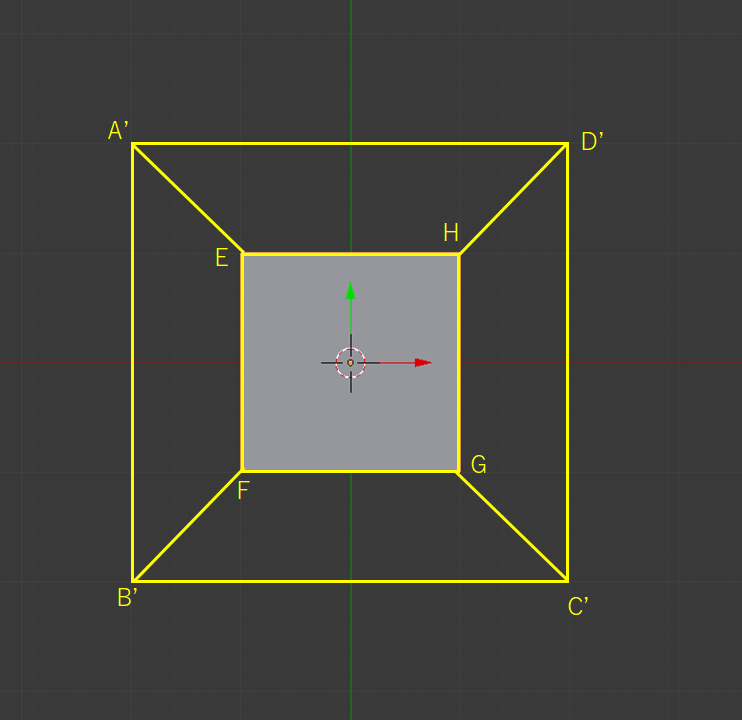
こうなります。愚かな2次元人には、上の図が描かれた紙を見せながらこう説明するとしましょう。
「どうだい? A'B'C'D'は正方形、EFGHも正方形であることはわかるだろう? 本当はその周りにある4つの四角形も正方形だけど、紙に書くにはこうするしかなかったんだ。全ての辺が同じ長さで、全ての辺が直角に交わっていると言っても信じられないかな。え? 正方形の中に正方形があるじゃないかって? 説明しづらいな……まあ君ら2次元人には理解できないか」
それでは次元を1つ上げてみよう
今度は愚かになるのは我々人間さんサイドになります。今度は4次元の図を3次元の図に投影します。とは言っても、4次元での描画は当然不可能なのでなにか方法を考えます。そこで、元々の3次元空間を圧縮して「平面」と考えると、次のような形で先程とまったく同じ投影を考えることができます。

こうして3次元世界に投影された4次元立方体が以下の図になります。

内側にある立方体が、上図で赤で描いた「平面」です。太陽から遠いため、その分「影」が小さいです。外側にある立方体が、上図で青で描いた「平面」です。太陽に近いため、その分「影」が大きいです。
数式で書くとこんな感じです。(※ 4次元目をとする)
四次元人(誰?)は上図の形をした立体を見せながらこう説明するでしょう。
「どうだい? 内側にあるのも立方体、外側にあるのも立方体であることはわかるだろう? 本当はその外側にある6つの立体も立方体だけど、この世界に持ってくるにはこうするしかなかったんだ。全ての辺が同じ長さで、全ての辺が直角に交わっていると言っても信じられないかな。え? 立方体の中に立方体があるじゃないかって? 説明しづらいな……まあ君ら3次元人には理解できないか」
更に次元を1つ上げるぞ
話はこれに留まりません。我々の目的は5次元なのですから。
今度は上の方法(ステレオ投影)は使えません。ステレオ投影を2回使ってもほとんど見た目が変わらないので意味がないからです。そこで今度は斜投影という方法を使います。と言っても、これはステレオ投影より簡単です。
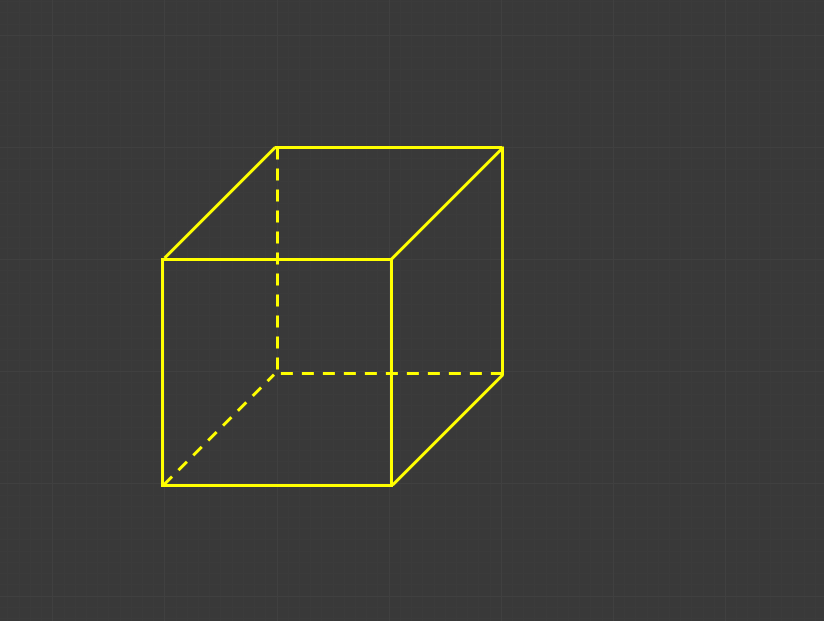
上の図もまた立方体ですが、左下の正方形が手前、右上の正方形が奥にあること、そしてナナメの成分が奥行きを表していることはすぐに分かると思います。これは「奥行きの分だけタテとヨコを足す」ことによって、立体を平面に表現しています。数式で書くとこんな感じです。
ここで、
- ステレオ投影
- 斜投影
という2つの方法で次元を2つ下げる方法がわかったので、これを組み合わせて
という変換により、5次元を3次元に圧縮することができます(※4,5次元目をとする)。その結果できたのがこちら。
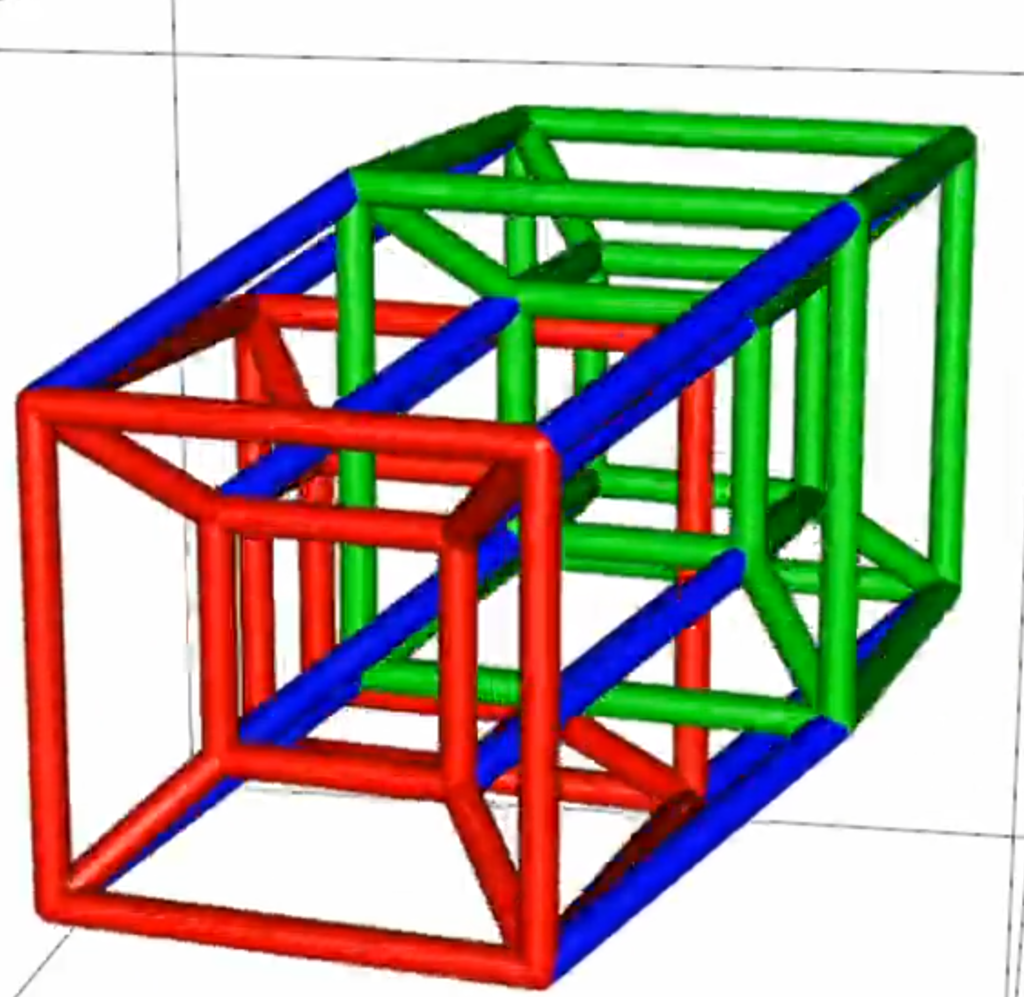
今までの説明を踏まえると、
- 赤色が斜投影上「手前」にある四次元立方体
- 緑色が斜投影上「奥」にある四次元立方体
であることが分かると思います。そして赤の「立方体」と緑の「立方体」を青い辺でつないだものもまた四次元立方体です。もちろん、全ての辺が同じ長さで、全ての辺は直角に交わっています。想像できるでしょうか?
これらを「回転」させと(5次元あるので、通りあります)以下のようになります。
VR界で4次元立方体がバズってるから私が作った5次元立方体ももうちょい流行ってもよくない? pic.twitter.com/unagNhuoqg
— Hibit (@hibit_at) 2018年9月6日
あなたは5次元立方体を理解できたでしょうか?