漸化式は平面上の線形変換だということ、あるいは非線形を多次元で殴る話
受験数学において三項間漸化式は頻出します。以下のようなやつ。
これを解くには、特性方程式を解いて式を比較して……というめんどくさい手続きをふまなければならないのですが、行列の対角化を使うことにより(計算量はともかく)手続き上はスムーズに解くことができます。
$$ \begin{bmatrix} a_{n+2} \\ a_{n+1}\\ \end{bmatrix}= \begin{bmatrix} 3 & -2 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} a_{n+1} \\ a_n\\ \end{bmatrix} $$
$$ \begin{bmatrix} a_{n+1} \\ a_n\\ \end{bmatrix}= \begin{bmatrix} 3 & -2 \\ 1 & 0 \\ \end{bmatrix}^{n-1} \begin{bmatrix} a_2 \\ a_1\\ \end{bmatrix} $$
$$ \begin{bmatrix} a_{n+1} \\ a_n\\ \end{bmatrix}= \begin{bmatrix} 1 & 2 \\ 1 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 2 \\ \end{bmatrix}^{n-1} \begin{bmatrix} -1 & 2 \\ 1 & -1 \\ \end{bmatrix} \begin{bmatrix} a_2 \\ a_1\\ \end{bmatrix} $$
$$ a_n= \begin{bmatrix} 1 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 2 \\ \end{bmatrix}^{n-1} \begin{bmatrix} -1 & 2 \\ 1 & -1 \\ \end{bmatrix} \begin{bmatrix} a_2 \\ a_1\\ \end{bmatrix} $$
$$ a_n= \begin{bmatrix} 1 & 2^{n-1} \\ \end{bmatrix} \begin{bmatrix} -a_1+2a_2 \\ a_1-a_2 \\ \end{bmatrix} $$
$$ a_n=-a_1+2a_2+2^{n-1}(a_1-a_2) $$
めでたしめでたし。テクニックだけを知りたいのならば、ここから先は読む必要はありません。
行列の意味するところ
$$ A=\begin{bmatrix} 3 & -2 \\ 1 & 0 \\ \end{bmatrix} $$
この行列が意味するところを考えていきます。の行列は平面上における座標変換、それも線形変換を示しています。
つまり、上の行列は
平面において
という点がどこからどこへ移動するかを示しているということになります。変換の様子を図示したものが下の図になります*1。
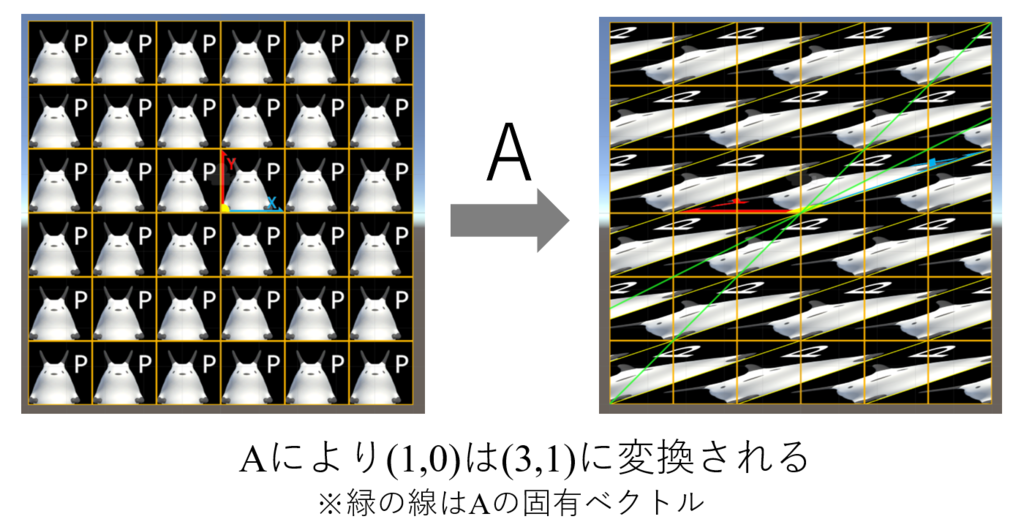
Aを作用させ続けると、がどのような動きをするかを図示したものが下になります。
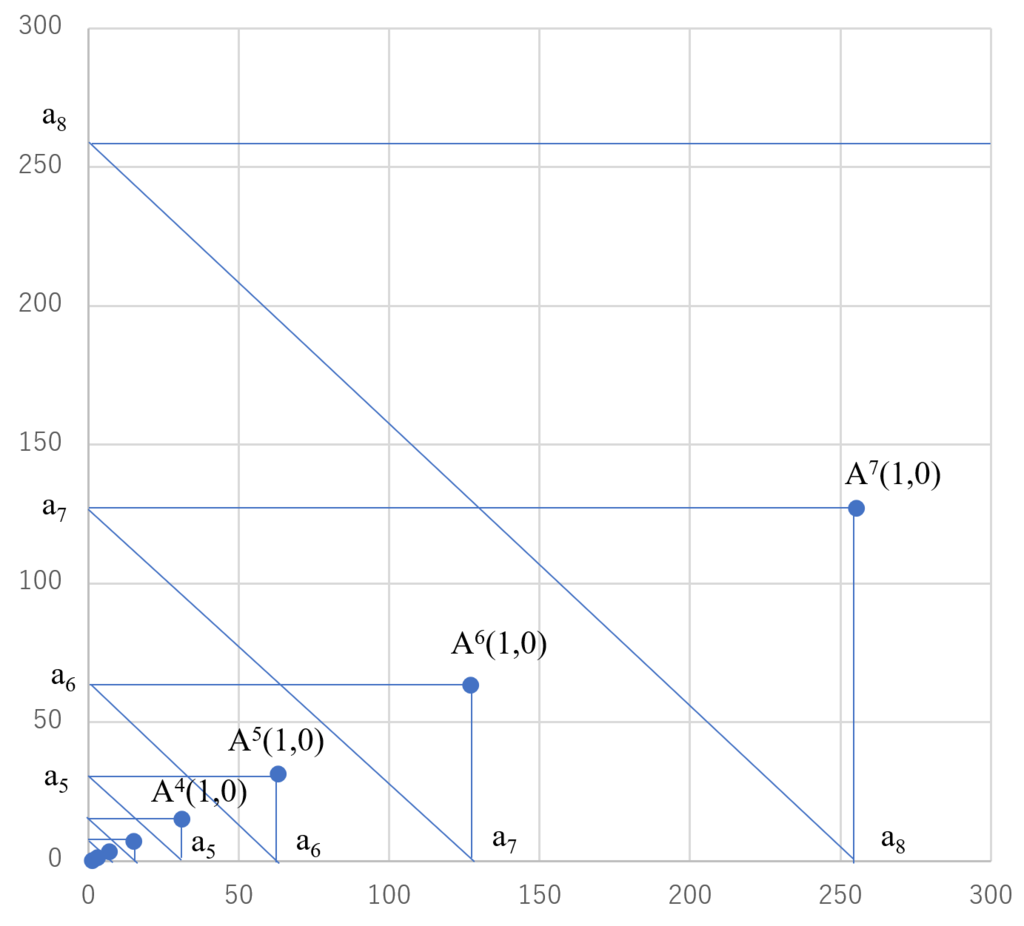
また、固有値を持つ線形変換は対角化によって直交基底の成分を抽出することができます。直交基底というとものものしいですが、要は「横方向にn倍、縦方向にm倍しているだけ」という状態です。見方を変えると、真の姿はそのようなシンプルな変換であるにも関わらず、何かの事情で、歪んだレンズを介してしか格子座標の世界に姿を現せないかわいそうな行列がであるともいえます(向こうからしたら我々の世界こそ
に歪んだ世界でしょうが)。その証拠に歪んだ座標に合わせた初期値を与えてやると以下の通り
$$ \begin{bmatrix} 3 & -2 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ \end{bmatrix}= \begin{bmatrix} 1 \\ 1 \\ \end{bmatrix}=1* \begin{bmatrix} 1 \\ 1 \\ \end{bmatrix} $$
$$ \begin{bmatrix} 3 & -2 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 2 \\ 1 \\ \end{bmatrix}= \begin{bmatrix} 4 \\ 2 \\ \end{bmatrix}=2* \begin{bmatrix} 2 \\ 1 \\ \end{bmatrix} $$
1倍、2倍されています。なんという素直な変換! お気づきの方も多いと思いますが、「n倍、m倍」は行列の固有値、「歪んだ座標に合わせた初期値」は行列の固有ベクトルに相当します。
固有値が重複する場合
漸化式の話に戻ると、特性方程式が重解を持つ場合があります。以下のようなやつ。
オーソドックスな手法だと、変数の数に対して方程式が足りなくなるため、で割るなどの小細工が必要になりますが、行列を用いた手法ならばそのようなものは必要ありません。
$$ \begin{bmatrix} a_{n+2} \\ a_{n+1}\\ \end{bmatrix}= \begin{bmatrix} 4 & -4 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} a_{n+1} \\ a_n\\ \end{bmatrix} $$
$$ \begin{bmatrix} a_{n+1} \\ a_n\\ \end{bmatrix}= \begin{bmatrix} 4 & -4 \\ 1 & 0 \\ \end{bmatrix}^{n-1} \begin{bmatrix} a_2 \\ a_1\\ \end{bmatrix} $$
$$ \begin{bmatrix} a_{n+1} \\ a_n\\ \end{bmatrix}= \begin{bmatrix} 2 & 1 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 2 & 1 \\ 0 & 2 \\ \end{bmatrix}^{n-1} \begin{bmatrix} 0 & 1 \\ 1 & -2 \\ \end{bmatrix} \begin{bmatrix} a_2 \\ a_1\\ \end{bmatrix} $$
多少ジョルってますが(註:完全な対角化が不可能であり、ジョルダン標準形を持つこと)計算は依然としてシンプルです。
$$ a_n= \begin{bmatrix} 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 2 & 1 \\ 0 & 2 \\ \end{bmatrix}^{n-1} \begin{bmatrix} 0 & 1 \\ 1 & -2 \\ \end{bmatrix} \begin{bmatrix} a_2 \\ a_1\\ \end{bmatrix} $$
$$ a_n= \begin{bmatrix} 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 2^{n-1} & (n-1)2^{n-2} \\ 0 & 2^{n-1} \\ \end{bmatrix} \begin{bmatrix} 0 & 1 \\ 1 & -2 \\ \end{bmatrix} \begin{bmatrix} a_2 \\ a_1\\ \end{bmatrix} $$
$$ a_n= \begin{bmatrix} 2^{n-1} & (n-1)2^{n-2} \\ \end{bmatrix} \begin{bmatrix} a_1 \\ a_2-2a_1 \\ \end{bmatrix} $$
$$ a_n=2^{n-1}a_1+(n-1)2^{n-2}(a_2-2a_1) $$
次元を上げて行列で殴る…定数項編
でもこの手法で扱えるのって線形変換だけじゃないの? と思った方へ。ご安心ください、以下のような非線形な式も次元を増やすことによって線形行列で殴ることができます。
行列形及び回答は以下の通り。
$$ \begin{bmatrix} a_{n+1} \\ 1\\ \end{bmatrix}= \begin{bmatrix} 2 & 1 \\ 0 & 1 \\ \end{bmatrix} \begin{bmatrix} a_n \\ 1\\ \end{bmatrix} $$
$$ \begin{bmatrix} a_n \\ 1\\ \end{bmatrix}= \begin{bmatrix} 2 & 1 \\ 0 & 1 \\ \end{bmatrix}^{n-1} \begin{bmatrix} a_1 \\ 1\\ \end{bmatrix} $$
$$ \begin{bmatrix} a_n \\ 1\\ \end{bmatrix}= \begin{bmatrix} -1 & 1 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 2 \\ \end{bmatrix}^{n-1} \begin{bmatrix} 0 & 1 \\ 1 & 1 \\ \end{bmatrix} \begin{bmatrix} a_1 \\ 1\\ \end{bmatrix} $$
$$ a_n= \begin{bmatrix} -1 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 2 \\ \end{bmatrix}^{n-1} \begin{bmatrix} 0 & 1 \\ 1 & 1 \\ \end{bmatrix} \begin{bmatrix} a_1 \\ 1\\ \end{bmatrix} $$
$$ a_n= \begin{bmatrix} -1 & 2^{n-1} \\ \end{bmatrix} \begin{bmatrix} 1 \\ a_1+1 \\ \end{bmatrix} $$
$$ a_n=-1+2^{n-1}(a_1+1) $$
ただこの手法、見かけはシンプルですけど計算量は多いです。対角化さえすればあとは単純ですが、そもそも対角化をするのが結構めんどうくさい。これだったらオーソドックスな特性方程式で解いた方が早いです。オシャレではあるけど実用性はないやつ。
次元を上げて行列で殴る…階差数列編
次元を上げれば非線形な漸化式も行列計算で解決できる! 今度はさらに発展させてみましょう。
いわゆる階差数列というやつ。
これも漸化式を分解することによって以下のように整理できます。
$$ a_{n+1}=a_n+b_n $$
$$ b_{n+1}=b_n+1 $$
$$ \begin{bmatrix} a_{n+1} \\ b_{n+1} \\ 1 \\ \end{bmatrix}= \begin{bmatrix} 1 & 1 & 0\\ 0 & 1 & 1\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} a_n \\ b_n \\ 1 \\ \end{bmatrix} $$
$$ \begin{bmatrix} a_n \\ b_n \\ 1 \\ \end{bmatrix}= \begin{bmatrix} 1 & 1 & 0\\ 0 & 1 & 1\\ 0 & 0 & 1\\ \end{bmatrix}^{n-1} \begin{bmatrix} a_1 \\ 1 \\ 1 \\ \end{bmatrix} $$
$$ \begin{bmatrix} a_n \\ b_n \\ 1 \\ \end{bmatrix}= \begin{bmatrix} 1 & n-1 & \frac{(n-1)(n-2)}{2}\\ 0 & 1 & n-1\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} a_1 \\ 1 \\ 1 \\ \end{bmatrix} $$
$$ a_n= \begin{bmatrix} 1 & n-1 & \frac{(n-1)(n-2)}{2}\\ \end{bmatrix} \begin{bmatrix} a_1 \\ 1 \\ 1 \\ \end{bmatrix} $$
$$ a_n=a_1+(n-1)+\frac{(n-1)(n-2)}{2} $$
$$ a_n=a_1+\frac{n(n-1)}{2} $$
このあたりになると、1次元直線における操作を3次元空間に写して計算していることになり、(この例では必要ないですが、大体の場合においては)逆行列の計算とかがエグいことになります。基本的に3次元以上の行列計算は人間のやることではないと考えています。GPUとかにやらせましょう。
補足1
タイトルに「平面上」とありますが、正確には「のユークリッド空間上」です。タイトルのわかりやすさを優先しました。
補足2
$$ a_{n+1}=a_n+b_n $$
$$ b_{n+1}=b_n+1 $$
を変形すると以下のような三項間漸化式(+定数項)になります。
$$ a_{n+2} = a_{n+1}+b_{n+1} $$
$$ a_{n+2} = a_{n+1}+b_n+1 $$
$$ a_{n+2} = a_{n+1}+(a_{n+1}-a_n)+1 $$
$$ a_{n+2} = 2a_{n+1}-a_n+1 $$
つまりこの2つの漸化式は、初期値の反映のされ方(つまり「歪み」)による見え方が違うだけで、本質的には同一のものであるといえます。実際に、得られるジョルダン標準形も同じです。
$$ \begin{bmatrix} 2 & -1 & 1\\ 1 & 0 & 0\\ 0 & 0 & 1\\ \end{bmatrix}= \begin{bmatrix} 1 & 1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 1 & 0\\ 0 & 1 & 1\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 0 & 1 & 0\\ 1 & -1 & 0\\ 0 & 0 & 1\\ \end{bmatrix} $$
例えば、という条件を満たす初期値ベクトルは、前者では
、後者では
という形になります。