Unityとレイマーチングを用いた射影平面上の二次曲線の可視化 Visualization of conic curve on projective plane using Unity and Raymarching hibit

f:id:hibit_at:20190130081525p:plain

概要

　二次曲線（楕円，放物線，双曲線）は3次元空間上の円錐に対して投影方向を変えた断面であると解釈できる．筆者は，ゲーム用ミドルウェアであるUnity上で，レイマーチングと呼ばれる技術を用いることにより，3次元空間上の円錐断面がある平面上で二次曲線になる様子，そしてその角度が変化する様子をリアルタイムに観察できるVR空間を作成し，それをVRゲーム「VRChat」上のワールドとして公開した．これにより，それぞれ別の形をしているように見える二次曲線が，射影平面上では無限遠を介して1つの円に対応していることを可視化した．

緒言

　以下，射影平面と二次曲線についての概説を記す．

射影平面

　ユークリッド空間 $\mathbb{R}^{n}$ 上において，原点を通る直線全体の集合（ただし原点を除く）は射影空間（Projective Space）と呼ばれ， $\mathbb{P}^{n-1}$ と表現される[1]．これは直感的には原点を通る直線の「傾き」だけを抽出した世界である．また，これら直線は原点を中心として球に対して対蹠点（反対側の点）を同一視した上で球面上の点に対応しており，それを平面に写したものは，ただの平面に加えて「無限遠で反対側にループする」性質を持つ平面であることがわかる[2]．

（射影平面の構造をシンプルに表現したもの．トポロジーへの招待 2 より引用）

　なお， $\mathbb{P}^{2}$ は $\mathbb{R}^{3}$ に埋め込めないことが知られているが[1]，自己交差した形では描画できる．そのような例として，例えば以下のようなCross-capと呼ばれる図形がある．

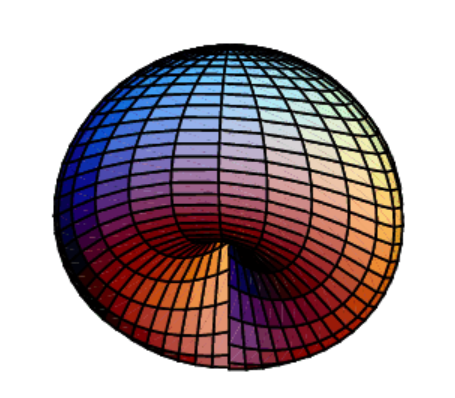
Cross-cap（Cross-Cap -- from Wolfram MathWorldより引用）

二次曲線

　楕円，放物線，双曲線はそれぞれ以下のような曲線である．

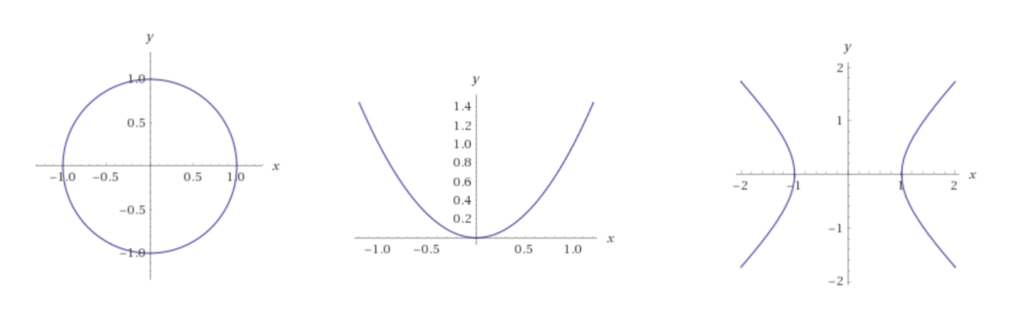（描画にはWolfram|Alpha: Computational Intelligenceを用いた）

　これらは，適当な定数 $a,b,c,d$ を用意することにより， $xy$ 空間上において， $$ ax^{2}+bxy+cy^{2}+d=0 $$ 　なる一般式により記述され，二次曲線（または円錐曲線，conic curve）と呼ばれる．

　これらは円錐の断面である正円を平面に写したものの，その角度を変えたものであるといえる．また，これらはすべてある円を異なる射影平面に投影したものであると言える．言い方を変えると，

楕円は傾いた「正円の影」
放物線は無限遠に伸びた「正円の影」
双曲線は無限遠を介して反対側にループする「正円の影」

　であると言える．

　上の事実は円錐を任意の平面で切った断面を計算することにより計算できる．つまり，原理的には，適当な定数 $p,q,r,s$ を用意することにより， $xyz$ 空間上において，

$$x^{2}+y^{2}-z^{2}=0$$ $$px+qy+rz+s=0$$

　を満たす $(x,y,z)$ を解析的に求めることにより，任意の二次曲線を生み出すことができる．

　しかし，実際にこれらの計算を解くことはかなり煩雑な作業であり，またそうして得られた二次方程式から平面と二次曲線との関係を直観することはやや困難である．そこで，ゲーム用ミドルウェアであるUnityを用いて「円錐が回転する様子」「円錐の延長と，ある平面の断面」を実際にゲーム画面上に描画することで，「任意の二次曲線が正円の影である」ことを可視化した．

　なお，楕円が円の影であることはほぼ自明であるが，放物線と双曲線が，無限遠を概念を加えた射影平面上においては円の影であると言えることについては，後の考察で説明する．

方法

　手法はレイマーチングと呼ばれる技術を用いた．これは，カメラポジションからレイ（探査線）を飛ばすことにより，レイがある条件を満たす時に座標を着色することにより，あたかも空間上にオブジェクトがあるかのような表現をするシェーダ技術である．

　本研究では，やぎり氏が公開しているコード[3]を一部改変し，以下の変更を加えた．

形状関数を球ではなく円錐にした
円錐を回転するようにした
角度によって色に変化を出すようにした
一定の距離を超えるとオブジェクトを描画しないようにした

　なお末尾の「付録」にソースコードを載せている．

結果

　実際に，VR空間上で円錐が回転し，それが平面に投影される様子を一人称視点で撮った動画が以下である．

　中心の球の中では赤・緑・青で着色された円錐が回転している．中心からの角度が同じであれば色相は同じになり，距離は問題にならない．つまり色相は空間上における線に対応する．これがある平面に投影される時，これは二次曲線となり色相は点に対応する．

　なお，見た目の都合上曲線だけではなくその内部も着色している．つまり元の正円における「円周」ではなく「円板」を描画しており，円板の中心に近ければ近いほど発光するような処理を加えている．

　このワールドは「Virtual Projective Plane」として，既にVRChat上にアップロードされているが，パフォーマンスの問題上パブリックワールドにはなっていない．いかに計算負荷を下げてパブリック申請を通すかというのもまた興味深いテーマであるが，それは今後の課題としたい．

考察

　上の現象を，射影平面の展開図上で考えてみる．射影平面は以下のようなトポロジーを持つ展開図を考えることができる[2]．

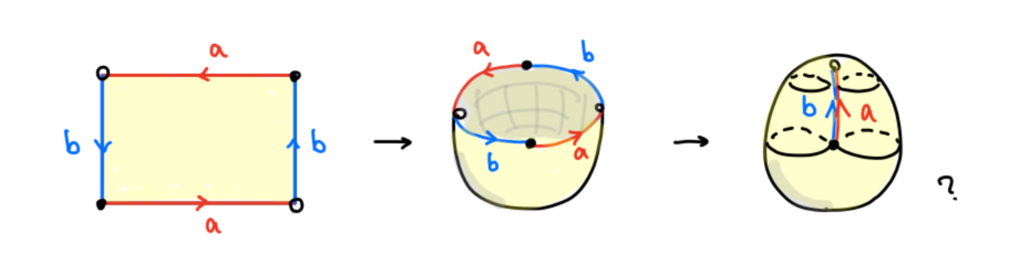（トポロジーへの招待 2 より引用）

　これらのつなぎ目を介して平面がループが連続する「大きな」平面を考える．家庭用RPG（つまりドラクエやその類）の世界であればこれは同一の平面が繰り返し続くだけだが（このような世界地図はトーラスと呼ばれるドーナツ型によって現実に再現できる），射影平面においてはループをする度に反対側に行く「ねじれ」が生じる．以下，射影平面の展開図にある同一の円が位置を変えながら投影される様子を示す．

f:id:hibit_at:20190203211808p:plain

　展開図の黄色の部分が観測者のいる世界であり，Unityの画面ではグリッドの刻まれた黒い床がそれにあたる．無限遠を越した後の世界では「ねじれ」が生じ，展開図ではそれを灰色の部分として示している（円のR→G→Bの方向が時計回りから反時計回りになっていることに注目されたい）．射影平面の展開図はこのように「ねじれ」を繰り返しながら永遠にループするものであり，1方向に限ればトポロジーとしてはメビウスの輪と同一となる．

　さて，床に投影された影に着目したい．円錐の直下に投影される円は当然ながら円となる．

　円錐の回転が進んだ時の様子を見る．

f:id:hibit_at:20190203212300p:plain

　この時，影は放物線となり，展開図では円が無限遠で接している（乱暴な定義で恐縮である）ことがわかり，放物線は無限遠に伸びた円であると言える．ただしこれは何も数十万kmも移動する，というものではなく，歪んだレンズを通して平面に写した結果，あたかも無限遠まで伸びるように「見えてしまう」，という方が本質に近い．円錐はただマイペースに回転しているだけである．

　更に円錐が回転する様子を見る．

f:id:hibit_at:20190203212929p:plain

　この時，影は双曲線となる．双曲線は2つに分かれた曲線ではなく，無限遠を介してつながった1つの円が写されたものである（と解釈できる）ことがわかる．青と緑の部分は，それぞれ無限遠を介して「反対側」にループする．

f:id:hibit_at:20190203213605p:plain

　更に回転が進むとまた放物線が現れる．

　この後はまた円→放物線→双曲線→放物線→…という変化が続くが，周期が180°ずれると映される円の色相が違う（時計回りと反時計回りとが逆転する）．この違いは単なる周期の違いでしかなく，メビウスの輪に表と裏がないようにどちらが正と言えるものではない．展開図においても，便宜上黄色を「表」，灰色を「裏」としているが，灰色側から見れば黄色こそが裏である．このように射影平面は向きつけ不可能なものである．

補足

　本記事はあたかも論文のような体裁を取ってはいるが，何の指導も査読も受けていないものである．記述内容に誤りがないか注意を払ってはいるが，内容（特にシェーダ，数学にかかわる部分）についてもし誤りがあれば，謹んで訂正したいので，筆者までお知らせ願いたい．このブログにはコメント欄がないので，お手数ながらtwitterのリプライかDMかで知らせていただきたい．

謝辞

　「方法」でも述べた通り，内容にクリティカルに関わる部分以外をやぎり氏のコードから流用させていただいている．また，レイマーチングを勉強し始める段階では，がとーしょこら氏には参考になるサイトをいくつも紹介いただいた．また，phi氏にはコード簡潔化のためのアドバイスをいただいた．この場を借りて感謝を申し上げたい．

参考文献

　著者名がハンドルネームしかわからない場合，はてなidを記す．

1, 松本幸夫（1988）「多様体の基礎」東京大学出版会．

2, 佐野岳人（2017）「トポロジーへの招待〜 2. 切り貼りで作る色々な曲面」http://taketo1024.hateblo.jp/entry/topology/2．

3 やぎり (id:yagiri000)（2018），「固定長進行レイマーチングやってみたので簡単なサンプルと解説」http://yagiri000.hatenablog.com/entry/2018/09/13/190006．

付録

　以下がシェーダのコードである．ベースは[2]より引用したコードであるが，いくつか改変を加えた．

Shader "Custom/ProjectivePlane"
{
    Properties
    {
        _Threshold("Threshold", Range(-0.1,0.1)) = 0 // sliders
        _BaseColor("BaseColor", Color) = (.5,.5,.5,1)
　　 }
    SubShader
    {
        Tags{ "Queue" = "Transparent" }
        LOD 100

        Pass
        {
            ZWrite On
            Blend SrcAlpha OneMinusSrcAlpha

            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag
            // make fog work
            #pragma multi_compile_fog

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 pos : POSITION1;
                float4 vertex : SV_POSITION;
            };

            v2f vert(appdata v)
            {
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.pos = mul(unity_ObjectToWorld, v.vertex);
                o.uv = v.uv;
                return o;
            }

            float _Threshold;
            float4 _BaseColor;
            float speed1;
            float speed2;

            float2x2 rotmat(float x){
                return float2x2(cos(x),-sin(x),sin(x),cos(x));
            }

            // 座標がオブジェクト内か？を返し，形状を定義する形状関数
            // 形状は原点を中心とした円錐．
            bool isInObject(float3 pos) {
                speed1 = _Time.x*3;
                speed2 = _Time.x*1.1;
                pos.xy = mul(rotmat(speed1),pos.xy);
                pos.zy = mul(rotmat(speed2),pos.zy);
                float keijou = pow(pos.x,2)+pow(pos.z,2)-pow(pos.y,2);
                return keijou < _Threshold;
            }

            fixed4 frag(v2f i) : SV_Target
            {
                fixed4 col;

                // 初期の色（黒）を設定
                col.xyz = _BaseColor;
                col.w = 1.0;

                // レイの初期位置
                float3 pos = i.pos.xyz; 

                // レイの進行方向
                float3 forward = normalize(pos.xyz - _WorldSpaceCameraPos); 

                // レイが進むことを繰り返す．
                // オブジェクト内に到達したら進行距離に応じて色決定
                // 当たらなかったらそのまま（今回は黒）
                const int StepNum = 1000;
                const float MarchingDist = 0.01;
                for (int i = 0; i < StepNum; i++) {
                    if (isInObject(pos)) {
                float3 original = pos.xyz;
                speed1 = _Time.x*3;
                speed2 = _Time.x*1.1;
                pos.xy = mul(rotmat(speed1),pos.xy);
                pos.zy = mul(rotmat(speed2),pos.zy);
                float light = saturate(1-(pow(pos.x,2)+pow(pos.z,2))*5);
                        if (pos.y>0){
                        col.xyz = (cos(atan2(pos.z,pos.x)+UNITY_PI*float3(0,2,4)/3)/2+light);
                        }
                        else{
                        col.xyz = (cos(atan2(pos.z,pos.x)+UNITY_PI*float3(3,5,7)/3)/2+light);
                        }
                        if (original.y < -.51){
                            col.xyz = _BaseColor;
                        }
                        if (pow(original.x,2) > pow(50.01,2)){
                            col.xyz = _BaseColor;
                        }
                        if (pow(original.z,2) > pow(50.01,2)){
                            col.xyz = _BaseColor;
                        }
                        break;
                    }
                    pos.xyz += MarchingDist * forward.xyz;
                }

                return col;
            }
            ENDCG
        }
    }
}

hibitの技術系メモ

数学とか3Dとか翻訳とか

Unityとレイマーチングを用いた射影平面上の二次曲線の可視化

概要

緒言

射影平面

二次曲線

方法

結果

考察

補足

謝辞

参考文献

付録