Unityとレイマーチングを用いた射影平面上の二次曲線の可視化

Unityとレイマーチングを用いた射影平面上の二次曲線の可視化 Visualization of conic curve on projective plane using Unity and Raymarching hibit

概要

　二次曲線（楕円，放物線，双曲線）は3次元空間上の円錐に対して投影方向を変えた断面であると解釈できる．筆者は，ゲーム用ミドルウェアであるUnity上で，レイマーチングと呼ばれる技術を用いることにより，3次元空間上の円錐断面がある平面上で二次曲線になる様子，そしてその角度が変化する様子をリアルタイムに観察できるVR空間を作成し，それをVRゲーム「VRChat」上のワールドとして公開した．これにより，それぞれ別の形をしているように見える二次曲線が，射影平面上では無限遠を介して1つの円に対応していることを可視化した．

緒言

　以下，射影平面と二次曲線についての概説を記す．

射影平面

　ユークリッド空間上において，原点を通る直線全体の集合（ただし原点を除く）は射影空間（Projective Space）と呼ばれ，と表現される[1]．これは直感的には原点を通る直線の「傾き」だけを抽出した世界である．また，これら直線は原点を中心として球に対して対蹠点（反対側の点）を同一視した上で球面上の点に対応しており，それを平面に写したものは，ただの平面に加えて「無限遠で反対側にループする」性質を持つ平面であることがわかる[2]．

（射影平面の構造をシンプルに表現したもの．トポロジーへの招待 2 より引用）

　なお，はに埋め込めないことが知られているが[1]，自己交差した形では描画できる．そのような例として，例えば以下のようなCross-capと呼ばれる図形がある．

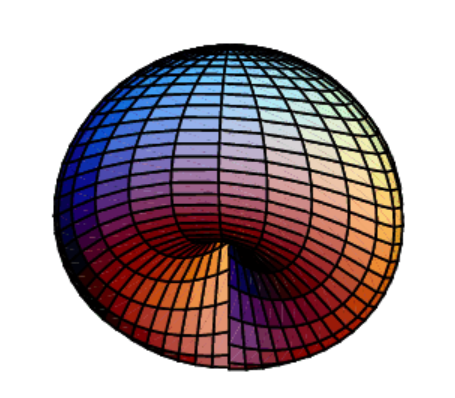
Cross-cap（Cross-Cap -- from Wolfram MathWorldより引用）

二次曲線

　楕円，放物線，双曲線はそれぞれ以下のような曲線である．

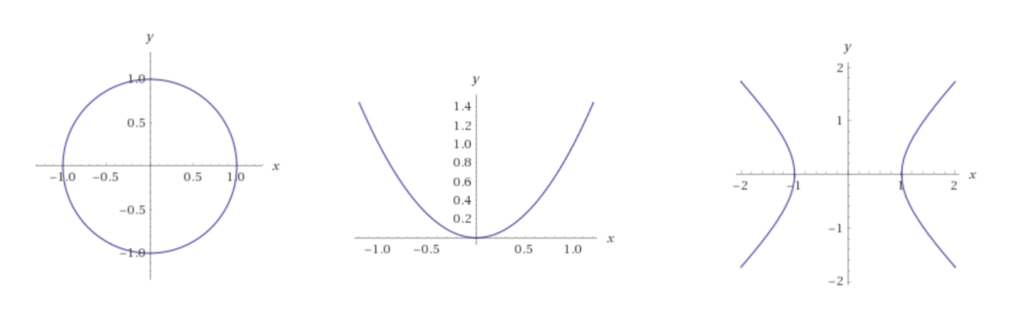（描画にはWolfram|Alpha: Computational Intelligenceを用いた）

　これらは，適当な定数を用意することにより，空間上において， $$ ax^{2}+bxy+cy^{2}+d=0 $$ 　なる一般式により記述され，二次曲線（または円錐曲線，conic curve）と呼ばれる．

　これらは円錐の断面である正円を平面に写したものの，その角度を変えたものであるといえる．また，これらはすべてある円を異なる射影平面に投影したものであると言える．言い方を変えると，

• 楕円は傾いた「正円の影」
• 放物線は無限遠に伸びた「正円の影」
• 双曲線は無限遠を介して反対側にループする「正円の影」

　であると言える．

　上の事実は円錐を任意の平面で切った断面を計算することにより計算できる．つまり，原理的には，適当な定数を用意することにより，空間上において，

$$x^{2}+y^{2}-z^{2}=0$$ $$px+qy+rz+s=0$$

　を満たすを解析的に求めることにより，任意の二次曲線を生み出すことができる．

　しかし，実際にこれらの計算を解くことはかなり煩雑な作業であり，またそうして得られた二次方程式から平面と二次曲線との関係を直観することはやや困難である．そこで，ゲーム用ミドルウェアであるUnityを用いて「円錐が回転する様子」「円錐の延長と，ある平面の断面」を実際にゲーム画面上に描画することで，「任意の二次曲線が正円の影である」ことを可視化した．

　なお，楕円が円の影であることはほぼ自明であるが，放物線と双曲線が，無限遠を概念を加えた射影平面上においては円の影であると言えることについては，後の考察で説明する．

方法

　手法はレイマーチングと呼ばれる技術を用いた．これは，カメラポジションからレイ（探査線）を飛ばすことにより，レイがある条件を満たす時に座標を着色することにより，あたかも空間上にオブジェクトがあるかのような表現をするシェーダ技術である．

　本研究では，やぎり氏が公開しているコード[3]を一部改変し，以下の変更を加えた．

• 形状関数を球ではなく円錐にした
• 円錐を回転するようにした
• 角度によって色に変化を出すようにした
• 一定の距離を超えるとオブジェクトを描画しないようにした

　なお末尾の「付録」にソースコードを載せている．

結果

　実際に，VR空間上で円錐が回転し，それが平面に投影される様子を一人称視点で撮った動画が以下である．

　中心の球の中では赤・緑・青で着色された円錐が回転している．中心からの角度が同じであれば色相は同じになり，距離は問題にならない．つまり色相は空間上における線に対応する．これがある平面に投影される時，これは二次曲線となり色相は点に対応する．

　なお，見た目の都合上曲線だけではなくその内部も着色している．つまり元の正円における「円周」ではなく「円板」を描画しており，円板の中心に近ければ近いほど発光するような処理を加えている．

　このワールドは「Virtual Projective Plane」として，既にVRChat上にアップロードされているが，パフォーマンスの問題上パブリックワールドにはなっていない．いかに計算負荷を下げてパブリック申請を通すかというのもまた興味深いテーマであるが，それは今後の課題としたい．

考察

　上の現象を，射影平面の展開図上で考えてみる．射影平面は以下のようなトポロジーを持つ展開図を考えることができる[2]．

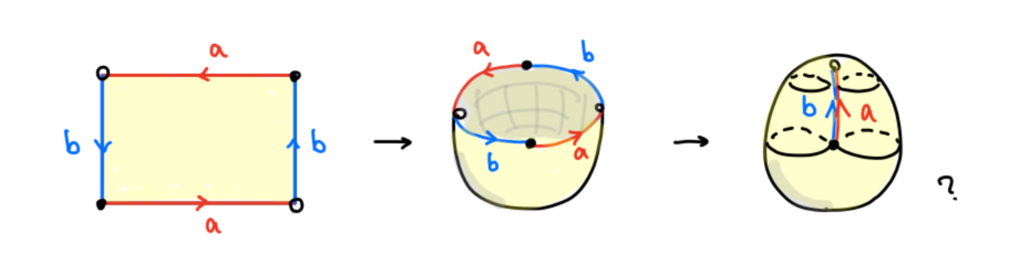（トポロジーへの招待 2 より引用）

　これらのつなぎ目を介して平面がループが連続する「大きな」平面を考える．家庭用RPG（つまりドラクエやその類）の世界であればこれは同一の平面が繰り返し続くだけだが（このような世界地図はトーラスと呼ばれるドーナツ型によって現実に再現できる），射影平面においてはループをする度に反対側に行く「ねじれ」が生じる．以下，射影平面の展開図にある同一の円が位置を変えながら投影される様子を示す．

　展開図の黄色の部分が観測者のいる世界であり，Unityの画面ではグリッドの刻まれた黒い床がそれにあたる．無限遠を越した後の世界では「ねじれ」が生じ，展開図ではそれを灰色の部分として示している（円のR→G→Bの方向が時計回りから反時計回りになっていることに注目されたい）．射影平面の展開図はこのように「ねじれ」を繰り返しながら永遠にループするものであり，1方向に限ればトポロジーとしてはメビウスの輪と同一となる．

　さて，床に投影された影に着目したい．円錐の直下に投影される円は当然ながら円となる．

　円錐の回転が進んだ時の様子を見る．

　この時，影は放物線となり，展開図では円が無限遠で接している（乱暴な定義で恐縮である）ことがわかり，放物線は無限遠に伸びた円であると言える．ただしこれは何も数十万kmも移動する，というものではなく，歪んだレンズを通して平面に写した結果，あたかも無限遠まで伸びるように「見えてしまう」，という方が本質に近い．円錐はただマイペースに回転しているだけである．

　更に円錐が回転する様子を見る．

　この時，影は双曲線となる．双曲線は2つに分かれた曲線ではなく，無限遠を介してつながった1つの円が写されたものである（と解釈できる）ことがわかる．青と緑の部分は，それぞれ無限遠を介して「反対側」にループする．

　更に回転が進むとまた放物線が現れる．

　この後はまた円→放物線→双曲線→放物線→…という変化が続くが，周期が180°ずれると映される円の色相が違う（時計回りと反時計回りとが逆転する）．この違いは単なる周期の違いでしかなく，メビウスの輪に表と裏がないようにどちらが正と言えるものではない．展開図においても，便宜上黄色を「表」，灰色を「裏」としているが，灰色側から見れば黄色こそが裏である．このように射影平面は向きつけ不可能なものである．

補足

　本記事はあたかも論文のような体裁を取ってはいるが，何の指導も査読も受けていないものである．記述内容に誤りがないか注意を払ってはいるが，内容（特にシェーダ，数学にかかわる部分）についてもし誤りがあれば，謹んで訂正したいので，筆者までお知らせ願いたい．このブログにはコメント欄がないので，お手数ながらtwitterのリプライかDMかで知らせていただきたい．

謝辞

　「方法」でも述べた通り，内容にクリティカルに関わる部分以外をやぎり氏のコードから流用させていただいている．また，レイマーチングを勉強し始める段階では，がとーしょこら氏には参考になるサイトをいくつも紹介いただいた．また，phi氏にはコード簡潔化のためのアドバイスをいただいた．この場を借りて感謝を申し上げたい．

参考文献

　著者名がハンドルネームしかわからない場合，はてなidを記す．

1, 松本幸夫（1988）「多様体の基礎」 東京大学出版会．

2, 佐野岳人（2017）「トポロジーへの招待 〜 2. 切り貼りで作る色々な曲面」http://taketo1024.hateblo.jp/entry/topology/2．

3 やぎり (id:yagiri000)（2018），「固定長進行レイマーチングやってみたので簡単なサンプルと解説」http://yagiri000.hatenablog.com/entry/2018/09/13/190006．

付録

　以下がシェーダのコードである．ベースは[2]より引用したコードであるが，いくつか改変を加えた．

Shader "Custom/ProjectivePlane"
{
    Properties
    {
        _Threshold("Threshold", Range(-0.1,0.1)) = 0 // sliders
        _BaseColor("BaseColor", Color) = (.5,.5,.5,1)
　　 }
    SubShader
    {
        Tags{ "Queue" = "Transparent" }
        LOD 100

        Pass
        {
            ZWrite On
            Blend SrcAlpha OneMinusSrcAlpha

            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag
            // make fog work
            #pragma multi_compile_fog

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 pos : POSITION1;
                float4 vertex : SV_POSITION;
            };

            v2f vert(appdata v)
            {
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.pos = mul(unity_ObjectToWorld, v.vertex);
                o.uv = v.uv;
                return o;
            }

            float _Threshold;
            float4 _BaseColor;
            float speed1;
            float speed2;

            float2x2 rotmat(float x){
                return float2x2(cos(x),-sin(x),sin(x),cos(x));
            }

            // 座標がオブジェクト内か？を返し，形状を定義する形状関数
            // 形状は原点を中心とした円錐．
            bool isInObject(float3 pos) {
                speed1 = _Time.x*3;
                speed2 = _Time.x*1.1;
                pos.xy = mul(rotmat(speed1),pos.xy);
                pos.zy = mul(rotmat(speed2),pos.zy);
                float keijou = pow(pos.x,2)+pow(pos.z,2)-pow(pos.y,2);
                return keijou < _Threshold;
            }

            fixed4 frag(v2f i) : SV_Target
            {
                fixed4 col;

                // 初期の色（黒）を設定
                col.xyz = _BaseColor;
                col.w = 1.0;

                // レイの初期位置
                float3 pos = i.pos.xyz; 

                // レイの進行方向
                float3 forward = normalize(pos.xyz - _WorldSpaceCameraPos); 

                // レイが進むことを繰り返す．
                // オブジェクト内に到達したら進行距離に応じて色決定
                // 当たらなかったらそのまま（今回は黒）
                const int StepNum = 1000;
                const float MarchingDist = 0.01;
                for (int i = 0; i < StepNum; i++) {
                    if (isInObject(pos)) {
                float3 original = pos.xyz;
                speed1 = _Time.x*3;
                speed2 = _Time.x*1.1;
                pos.xy = mul(rotmat(speed1),pos.xy);
                pos.zy = mul(rotmat(speed2),pos.zy);
                float light = saturate(1-(pow(pos.x,2)+pow(pos.z,2))*5);
                        if (pos.y>0){
                        col.xyz = (cos(atan2(pos.z,pos.x)+UNITY_PI*float3(0,2,4)/3)/2+light);
                        }
                        else{
                        col.xyz = (cos(atan2(pos.z,pos.x)+UNITY_PI*float3(3,5,7)/3)/2+light);
                        }
                        if (original.y < -.51){
                            col.xyz = _BaseColor;
                        }
                        if (pow(original.x,2) > pow(50.01,2)){
                            col.xyz = _BaseColor;
                        }
                        if (pow(original.z,2) > pow(50.01,2)){
                            col.xyz = _BaseColor;
                        }
                        break;
                    }
                    pos.xyz += MarchingDist * forward.xyz;
                }

                return col;
            }
            ENDCG
        }
    }
}

VRChatを目的にする人、VRChatを手段にする人

（どちらが優れているとかどちらが劣っているとか、そういう話ではないですよ。念の為。）

　どうも、hibitです。去年の12月～今年の1月にかけて今更ながらBeat Saberにハマっていました。と言っても、難譜面攻略や高ランクを目指す訳ではなく、人類がまだ経験していない芸術アートである（と勝手に思っている）逆手セイバーを確立・普及させるという使命（であると勝手に思っている）を果たすべく、

• MODの導入
• トラッカーの購入
• バーチャルモーションキャプチャー（VMC）の導入
• VMCを合成する為にLIVを導入
• マッピング（譜面作成）
• 動画編集

　などの環境構築・技術習得を主に行っておりました。という訳で動画観て。

座頭市のテーマをBeatSaber用の譜面にマッピングしました。
たぶんほぼ間違いなく世界初・逆手用のビートセイバー譜面です。
マッピングもそうだけどプレイングもだいぶ頑張った（つかれた）。
YouTube→https://t.co/H9aKef9w0c#BeatSaber#バーチャルモーションキャプチャー pic.twitter.com/s80rNxbD7J

— Hibit (@hibit_at) 2019年1月13日

　これらの活動をできたのは、えんぢょ氏がdiscord鯖に誘ってくれたことが大きくて、この場を借りて感謝の念を申し上げます。また、技術面においてはチャイロ氏（100万再生おめでとう！）にはいつも素早いお返事をいただきました。ほか個別に名前をあげていくとキリがないので割愛させていただきますが、皆様にはお世話になりました。ありがとうございました。

　そうそう、チャイロ氏の動画、100万再生超えたんですよね。すごい！

絶対にクリアしたい曲が出来たんですが、片手ダースモールじゃいい加減譜面の速度に腕が追い付かない😇
腰トラ抜いて左手に移植し、部分部分で両手を使うことを覚えようと思います。多分左手の問題も解決するはず。したらいいなあ
それはそれとして背面斬りけっこうキメられたのでまぁまぁ満足(*‘∀‘) pic.twitter.com/fYDZX6ZZHi

— チャイロ (@BeatDarth) 2019年1月4日

　先日、それをお祝いしてVRChat（VRC）上でバーチャルオフ会的なのが開催されました。

※バーチャルプライバシーに配慮してバーチャル目線を入れています（意味あるのか？）

　一瞬で集まれて、離席も気兼ねなくできて、それでいて空気はオフ会そのもの。いやあ実に便利な世の中になったものだ。

　実は上に書いたことはすべて報告・宣伝・前置きで、その時に感じたことが本記事の内容になります。VRCには、それを目的にする人と、それを手段にする人とがいるということです。

VRCを目的とする人

　私のVRキャリア（？）はVRChatから始まっていまして、2018年の4月からのものになります。その頃は、まだ販売アバターも豊富ではなく、アバターといえば改変（というかミコちゃん）か自作かという感じでした。当然、アバターの自作は、

• ポリゴン編集
• リグ付け
• UV展開
• テクスチャ付け
• Unityでの調整

　といった長大な手間を要するものであり、その過程で自然にその人のこだわり・創造性、言ってしまえば「魂」が宿るものでした。

　当然、そのような状況では、VRCで出会った人との会話もアバターに関するものが多くなり、「アバターが自作かどうか」「シェーダは何を使っているか」というものはとっかかりとして定番でした。また、アバター以外の話題であっても、ワールド作成であるとか、どのようなVRデバイスを使っているか、というものになりやすかったと記憶しています。

　このような状況は、VRCにいるだけでどんどん情報共有がなされ進化が起こりやすく、それがまたさらなる進化を……という好循環を生み出しやすく、そのおかげでVRCには活発なコミュニティ群がいくつも出来ていました（今も出来ているのかもしれませんが、あまり把握できていない……）。つまりVRCそのものがVRCにいる目的になっていた訳です。今のVRCにある豊富なアバターとワールドは、こういった空気の中で色々な人達が切磋琢磨してきたからこそ成り立ってきたものなのだと思います。私も、あの時期にVRCを初めていなかったら、自分でフルスクラッチアバターを作ったりすることはなかったかもな、と今でも思います。

　ただその一方で、「VRCで話すことが、本質的にはVRCに関わること（あとそれにまつわる人間関係とか）以外あまりない」という状況が長く続くことに、少し息苦しさを覚えていたのかもしれません。

VRCを手段とする人

　ここで話を冒頭で話したバーチャルオフ会に戻しますと、そこではVRCに慣れていない人がほとんどでした。joinてなに、フレンド申請ってどうやるの、というそういうレベル。当然、私含むVRC慣れてる勢が先導してアテンド的な働きをやっていました。と言っても、全然嫌ではなかったというか、むしろ新鮮な感じでした。

　アバターも、アバターワールドで借りてきたもので通して、特にそれで十分。VRCに入るのに、別にBlenderやUnityと格闘することは必要条件でも何でもない、という当たり前の事実を改めて感じることになりました（VRCのヘビーユーザーのグループにいると時々忘れそうになります）。こういう空気に触れると、VRC界隈で論争になっていたこと（自作アバター至上主義とかね）がばからしく思えてくる程ですが、こういう気軽な楽しみ方こそ、技術が本来目指すべきものではないのかな、とも思います。

　今後、このようなツールとしてのVRC（もしくは他のVR/ARプラットフォーム）の活用はどんどん進んでいくでしょう。そこでは、アバターもワールドも単なる手段であり、その人の魂を顕現させるものではありません。

それは良いことなのか悪いことなのか

　長期的には良いことだと思います。というのも、自己目的化した同質的な集団は、高い付加価値を生み出しやすい反面、過激化しやすい・排他的になりやすいという側面があります。ライト層の参入は、そういったタコツボ性を壊し、文化を一般化・長寿命化させるという働きがあります。

　そりゃ、いわゆる「古参」「懐古」側の気持ちはわからんでもないですよ。大衆化するとノイズが増えます。事実、インターネットは大衆化してゴミだらけの腐海になりました。パソコン通信の時代や、5ちゃんねる（旧2ch）の時代で時が止まって欲しいという人もいるでしょうが、やはり今のインターネットの利便性があるのは、色々なユーザーを取り込んで拡大してきたからです。それに、腐海の中でも情報を真摯に発信している人はいます。このブログもそうでありたいと願っています。全然関係ないけど、クソみたいなまとめサイトとかコタツ記事とか早く絶滅しないかな。

　いまだ発展途上にあるVR/AR界隈においても、ギーク層もライト層もお互いを尊重しつつ長く共存していけるといいですね、という超無難なまとめで本記事を締めたいと思います。

　そう言えば、Beat SaberもVRゲームのはずだけどあまりVR文化という感じがないですね。根本的に音ゲー文化だから？

アニメーションオーバーライドによって中腰になってしまったアバターを直す方法（Unity2017用）

　以前紹介していたアバターの中腰解除方法ですが、

deux-hibi.hatenablog.com

　なんと、VRChatに対応したUnityのバージョンが5.6.3から2017.4.15に上がったことにより、上記事の方法1が使えなくなってしまいました。

　それに合わせて記事をリライトしようと思いましたが、タイミングがいいことにがとーしょこらさんがワンクリックで中腰を解除できるツール（VRCDeveloperTool）を公開してくれたので、その紹介を改めて行うような形で新記事としたいと思います。これを専門用語で他力本願と言います。

導入及び操作方法

　先程リンクを貼ったページからダウンロード。

　無料でもDLできますけど、当然お前らもブーストで投げ銭するよな？（私はしました）

　DLしたファイルをAssets欄にドラッグ＆ドロップ。今からこの中腰になったAlcedoちゃんを救出します。

　ドロップした後は、Unityの上の方にあるメニューバーに「VRCDeveloperTool」という欄が出来ているはずなので、そこにある「HumanoidPose Resetter」をクリック。

　でてきたウィンドウにある「TargetObject」に、中腰を直したいアバターのオブジェクト（リグやメッシュではなく、親のオブジェクトです）をドラッグ＆ドロップ。

「Reset Pose」を押すと、この通り。めでたしめでたし。

　…。

　……。

　聴こえるぞ……ツールに頼らずに中腰を抹殺したいという怨嗟の叫びが……！

心を込めて中腰を抹殺する方法

　前記事の焼き直しになりますが、おさらい。

　Unityのアセット欄をたどって、

Assets > VRCSDK > Examples > Sample Assets > Animation

　の中にある「tpose-new」の横にある小さな再生ボタンを押します。

　そうしたらその横に「tpose-new」というアニメーションファイルが出てくると思うので、それを選択した状態でアニメーションウィンドウを押すと、 　

　このように、夥しい数のアニメーションコンポーネントが出てきます。これを全部コピーして、元々あった（つまり中腰の原因になっていた）アニメーションにペーストします。これで解決！

　……と、前記事のコピペで終わるのもアレなので補足的なあれこれ。

Tポーズの動きを入れたら、アニメーション中も強制的にTポーズになったりしないの？

　なりません。VRCをプレイしている最中は、ボーンの動きはすべてトラッキングに準拠します。

全部のアニメーションにTポーズの動きを入れると煩雑なんだけど

　再生ボタンを押して発動するアニメーションは、Animatorの「Entry」から矢印が出ているオレンジ色のアニメーションになります。そこにTポーズの動きを入れていれば、再生中は（そして何か変なことをしなければ再生後も）Tポーズになります。

　更に、オーバーライド用のアニメーションに一切余計なプロパティを入れたくないということであれば、下の図ようにTポーズ用のアニメーションを用意して、Entryからそこに矢印を飛ばすようにしましょう。

　上の図でいうと「Wink」「Buku」がオーバーライドさせたいアニメーションになります。

再生中はTポーズにできても、再生を止めるとまた中腰になるんだけど

　Tポーズのアニメーションウィンドウで、

　この録画ボタンを2回押すと操作画面でもTポーズに戻ると思います。

　だが勇者よ油断するな、Unity2017を倒しても、Unityのアップデートが続く限り、第二第三の中腰がまたお前たちを襲うであろう……。

フェルマーの最終定理もどき

　先日、あるフォロワーさんがこのようなツイートをしていました。

（晒し上げる意図はないので、ID等は伏せています）

　nが自然数だったら有名なフェルマーの最終定理ですが、nが自然数じゃなかったら普通に成り立ちそうですね。という訳で私が考えた解答が以下の通り。

n∈Cなら成立するな pic.twitter.com/lwnNoRRTmn

— Hibit (@hibit_at) 2018年12月21日

　本当の問題はこれからで、ドヤ顔であげたはいいものの、上の解答には数字の間違いがあります。よくやるんだこういうミス……。元ツイートのリプ欄には補足を入れていますが、ではなくが正です。間違い正しついでに清書と解説を加えておきます。

清書

証拠

　ホントかよ、と思う方へ。Wolframに実際に計算してもらいました。

解説

　上の解答を見ただけで納得できる人となんのこっちゃという人との両方がいると思うので、解説を加えます。上のトリック（？）は実数を虚数乗すると三角関数になるという仕組みを利用したものです。理由なんて聞かないで。今夜はずっと側にいて。もしくはマクローリン展開でぐぐって。式にすると以下になります。

　これを図示すると、下図のようなめかぶのバケモノみたいな曲面2種類（実部と虚部）、になりますが、の断面でスパッと切るとおなじみの三角関数になります。

　しかも、この三角関数はどのような実数をかけても振幅が同じであるという特性があります。振幅が変わらない代わりに周期が変わります。

　実数の虚数乗は実部と虚部とで単位円の座標になるので、単位円同士でが成り立つような組み合わせを見つければ上記のフェルマーもどきを満たす等式は見つかるという訳です。そのようなものには、例えばがあるので、それに対応した実数とを用意すれば出来上がりです。

　ただ、だとを満たさないので、三角関数の周期はを足しても変わらない、という性質を利用してにしています。こうして見るとえらい強引だ……！

　ちなみに、上の計算に「オイラーの等式」として有名な下の式が出てきますが、

　要するに、回したら、単位円上のの位置になるよ、という幾何学的にはごく単純なことを述べているに過ぎないことがわかります。

冷静なつっこみ

　その後、あーあーあ～さんから冷静なつっこみが入る。

これn∈Rで十分だと思う　x,y,zを割と適当にとっても中間値の定理からnの存在が示せるのであとはn>3となるようにすればよい（例えば(x,y,z)=(4,4,5)など）　さらにx=yとしておけば陽に解ける

— あーあーあ～ (@aaavrc) 2018年12月22日

　……。

　確かに、であり、またなので、のどこかで必ずであるようなは存在することになります。なお、これは容易に解けてとなります。

　ええーい、誰だ誰だ複素数なら成り立つ（ﾄﾞﾔ　とか言ってたやつは。

　無駄に話を複雑にする男ってどこにでもいるよね～、という話でした。

Photoshop持ってなくてもpsdファイルがあるとテクスチャ改変する時に便利だという話

　今回はCGをやっている人からすると鼻で笑われるような話ですが、適当にぐぐった感触だと言及している記事がなかったので一応書いておきます。

アバターをテクスチャ改変したいとき

　アバターを改変するにあたって一番手頃な方法はテクスチャ改変（色変え）だと思います。だいたいの画像編集ソフトには色調補正（色相・輝度・彩度をいじる機能）がついているので、テクスチャ画像（pngファイル）のうち色を変えたい部分を範囲選択して色調補正する、というのがオーソドックスな方法かと思います。

　しかしこれには実は2つのデメリットがあります。

• 範囲を選択するのがめんどくさい
• ワークフローが直列かつ破壊的である

　レイヤー管理されたファイル（ほとんどの場合はPhotoshop用のデータであるpsdファイル）を使うことにより、これらのデメリットを解消することができます。でもワイPhotoshopなんてハイカラなモン持ってへんし……と思っているあなた、psdファイルはフリーソフトのgimpでも開けるので大丈夫です。これから先は実際にgimpの操作画面を交えながら解説していきます。

範囲を選択しやすい

　これから先は、この間製作者であるみにさんの許可をいただけたので、実際の販売モデルである

miniscape.booth.pm

　みかちゃんのテクスチャで説明していこうと思います。みにさんありがとう！　なななんとこのかわいいモデルが2,100円！　買うしかない！　時代の波に乗り遅れるな！　マストバイ！

　で、これが実際のテクスチャ。psdファイルをgimpで開いています。

　右にあるレイヤーウィンドウで、このテクスチャ画像がいくつかのレイヤーに分かれていることがわかります。例えば、ハートの色をピンクから青に変えたい時は、

　ハートのレイヤーの色全体を変えれば、ハートの色だけが変わります。わざわざ範囲の選択や色域の選択で頑張る必要はなかった！　というだけでなく、もう1つのメリットも紹介します。というか、こちらの方がより大事かなと。

直列かつ破壊的なワークフロー

　ある画像に対して

1. 編集→その結果を反映
2. 更にそれを編集→その結果を反映
3. 更にそれを編集→その結果を反映

　という風に編集していくのは直列的なワークフローです。3番目の操作をした後で、2番目の操作だけを変えてみた結果を見たい、ということはアンドゥ等で遡らない限り不可能です。また、遡って2番目の操作を修正した後で3番目の操作を繰り返すのはひどく徒労感を伴います。

　そうでなくとも、色合いを変えた後で光沢もつけたいし、色合いもベースカラーと調整用の色を分けたいし……という状況が考えられますし、それぞれの効き具合も独立に確かめたいところです。

　また、pngで上書き保存してしまったら、もう元のファイルには二度と戻せません。そもそも緑色にしたいよね、となっても、もう青色になってしまったファイルしかないのです。元データや作業履歴を残すためには、別にファイルを用意してバージョン管理……とやる必要がありますが、まあスマートではないですよね。

　図で表すとこんな感じ。

並列かつ非破壊的なワークフロー

　レイヤーを使うと複数の操作を並列的に処理することができます。

　レイヤーウィンドウで右クリックして「新しいレイヤーグループ」を作成。

　でてきたグループ（例では「ハートG」と名付けています）にハートレイヤーを格納させた後、その中で「新しいレイヤーの追加」を行う。

　この時にレイヤーの描画モードを「標準」ではなく「乗算」にします。とりあえずは色を足すなら「乗算」、明るくするなら「加算」と覚えておいて、他のモードの細かい違いは慣れてきたら気にしていく感じでいいと思います。

　影や光を足していくとこんな感じ。それぞれの操作がレイヤーで分かれているのがわかるかと思います。

　図で表すとこんな感じ。

　各操作はレイヤーとして独立しているので、その調整にあたって順番を気にする必要はありません。また、元データはオリジナルレイヤーとして残されているので、いくら改変をしても元データに戻るのは容易です。例えるなら、電卓だと途中で1つでも打ち間違えたら終わりですけど、関数電卓だと途中の式を変えて計算結果を変えることができますよね。あんな感じです。余談になりますが私は以上のような理由により（破壊的編集プロセスの塊である）電卓が大嫌いです。

　テクスチャのごく簡単な改変でも、作業の途中で絶対にあ……これ戻りたいとか前やったあそこのパラメータだけ変えたいなとか思ったりすることはあります。元のデータには手を加えず、レイヤー管理ですべて済ませるという考え方を持つと、選択範囲を絞る労力も必要もないし、ムダなく作業ができますよという話でした。

漸化式は平面上の線形変換だということ、あるいは非線形を多次元で殴る話

　受験数学において三項間漸化式は頻出します。以下のようなやつ。

　これを解くには、特性方程式を解いて式を比較して……というめんどくさい手続きをふまなければならないのですが、行列の対角化を使うことにより（計算量はともかく）手続き上はスムーズに解くことができます。

$$ \begin{bmatrix} a_{n+2} \\ a_{n+1}\\ \end{bmatrix}= \begin{bmatrix} 3 & -2 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} a_{n+1} \\ a_n\\ \end{bmatrix} $$

$$ \begin{bmatrix} a_{n+1} \\ a_n\\ \end{bmatrix}= \begin{bmatrix} 3 & -2 \\ 1 & 0 \\ \end{bmatrix}^{n-1} \begin{bmatrix} a_2 \\ a_1\\ \end{bmatrix} $$

$$ \begin{bmatrix} a_{n+1} \\ a_n\\ \end{bmatrix}= \begin{bmatrix} 1 & 2 \\ 1 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 2 \\ \end{bmatrix}^{n-1} \begin{bmatrix} -1 & 2 \\ 1 & -1 \\ \end{bmatrix} \begin{bmatrix} a_2 \\ a_1\\ \end{bmatrix} $$

$$ a_n= \begin{bmatrix} 1 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 2 \\ \end{bmatrix}^{n-1} \begin{bmatrix} -1 & 2 \\ 1 & -1 \\ \end{bmatrix} \begin{bmatrix} a_2 \\ a_1\\ \end{bmatrix} $$

$$ a_n= \begin{bmatrix} 1 & 2^{n-1} \\ \end{bmatrix} \begin{bmatrix} -a_1+2a_2 \\ a_1-a_2 \\ \end{bmatrix} $$

$$ a_n=-a_1+2a_2+2^{n-1}(a_1-a_2) $$

　めでたしめでたし。テクニックだけを知りたいのならば、ここから先は読む必要はありません。

行列の意味するところ

$$ A=\begin{bmatrix} 3 & -2 \\ 1 & 0 \\ \end{bmatrix} $$

　この行列が意味するところを考えていきます。の行列は平面上における座標変換、それも線形変換を示しています。 つまり、上の行列は平面においてという点がどこからどこへ移動するかを示しているということになります。変換の様子を図示したものが下の図になります*1。

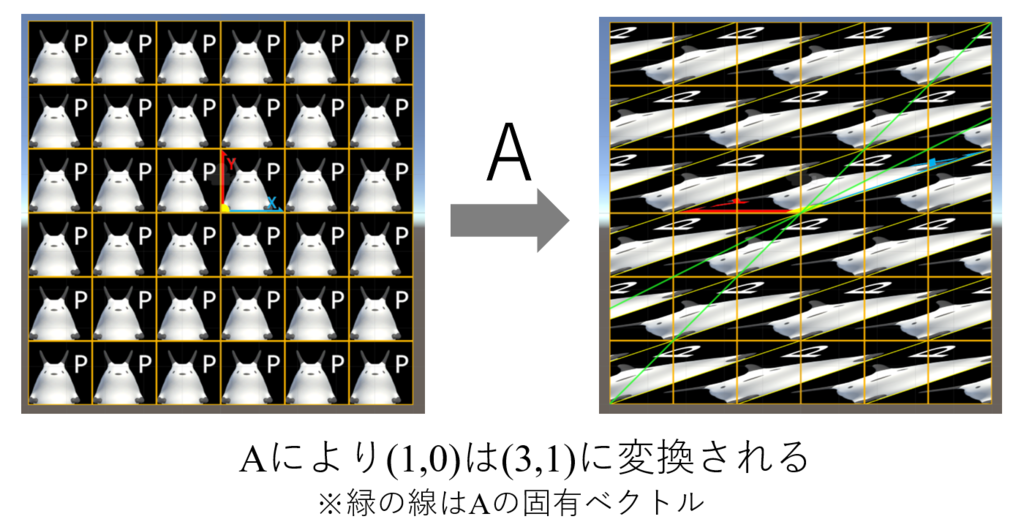
　Aを作用させ続けると、がどのような動きをするかを図示したものが下になります。

　また、固有値を持つ線形変換は対角化によって直交基底の成分を抽出することができます。直交基底というとものものしいですが、要は「横方向にn倍、縦方向にm倍しているだけ」という状態です。見方を変えると、真の姿はそのようなシンプルな変換であるにも関わらず、何かの事情で、歪んだレンズを介してしか格子座標の世界に姿を現せないかわいそうな行列がであるともいえます（向こうからしたら我々の世界こそに歪んだ世界でしょうが）。その証拠に歪んだ座標に合わせた初期値を与えてやると以下の通り

$$ \begin{bmatrix} 3 & -2 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ \end{bmatrix}= \begin{bmatrix} 1 \\ 1 \\ \end{bmatrix}=1* \begin{bmatrix} 1 \\ 1 \\ \end{bmatrix} $$

$$ \begin{bmatrix} 3 & -2 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 2 \\ 1 \\ \end{bmatrix}= \begin{bmatrix} 4 \\ 2 \\ \end{bmatrix}=2* \begin{bmatrix} 2 \\ 1 \\ \end{bmatrix} $$

　1倍、2倍されています。なんという素直な変換！　お気づきの方も多いと思いますが、「n倍、m倍」は行列の固有値、「歪んだ座標に合わせた初期値」は行列の固有ベクトルに相当します。

固有値が重複する場合

　漸化式の話に戻ると、特性方程式が重解を持つ場合があります。以下のようなやつ。

　オーソドックスな手法だと、変数の数に対して方程式が足りなくなるため、で割るなどの小細工が必要になりますが、行列を用いた手法ならばそのようなものは必要ありません。

$$ \begin{bmatrix} a_{n+2} \\ a_{n+1}\\ \end{bmatrix}= \begin{bmatrix} 4 & -4 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} a_{n+1} \\ a_n\\ \end{bmatrix} $$

$$ \begin{bmatrix} a_{n+1} \\ a_n\\ \end{bmatrix}= \begin{bmatrix} 4 & -4 \\ 1 & 0 \\ \end{bmatrix}^{n-1} \begin{bmatrix} a_2 \\ a_1\\ \end{bmatrix} $$

$$ \begin{bmatrix} a_{n+1} \\ a_n\\ \end{bmatrix}= \begin{bmatrix} 2 & 1 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 2 & 1 \\ 0 & 2 \\ \end{bmatrix}^{n-1} \begin{bmatrix} 0 & 1 \\ 1 & -2 \\ \end{bmatrix} \begin{bmatrix} a_2 \\ a_1\\ \end{bmatrix} $$

　多少ジョルってますが（註：完全な対角化が不可能であり、ジョルダン標準形を持つこと）計算は依然としてシンプルです。

$$ a_n= \begin{bmatrix} 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 2 & 1 \\ 0 & 2 \\ \end{bmatrix}^{n-1} \begin{bmatrix} 0 & 1 \\ 1 & -2 \\ \end{bmatrix} \begin{bmatrix} a_2 \\ a_1\\ \end{bmatrix} $$

$$ a_n= \begin{bmatrix} 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 2^{n-1} & (n-1)2^{n-2} \\ 0 & 2^{n-1} \\ \end{bmatrix} \begin{bmatrix} 0 & 1 \\ 1 & -2 \\ \end{bmatrix} \begin{bmatrix} a_2 \\ a_1\\ \end{bmatrix} $$

$$ a_n= \begin{bmatrix} 2^{n-1} & (n-1)2^{n-2} \\ \end{bmatrix} \begin{bmatrix} a_1 \\ a_2-2a_1 \\ \end{bmatrix} $$

$$ a_n=2^{n-1}a_1+(n-1)2^{n-2}(a_2-2a_1) $$

次元を上げて行列で殴る…定数項編

　でもこの手法で扱えるのって線形変換だけじゃないの？　と思った方へ。ご安心ください、以下のような非線形な式も次元を増やすことによって線形行列で殴ることができます。

　行列形及び回答は以下の通り。

$$ \begin{bmatrix} a_{n+1} \\ 1\\ \end{bmatrix}= \begin{bmatrix} 2 & 1 \\ 0 & 1 \\ \end{bmatrix} \begin{bmatrix} a_n \\ 1\\ \end{bmatrix} $$

$$ \begin{bmatrix} a_n \\ 1\\ \end{bmatrix}= \begin{bmatrix} 2 & 1 \\ 0 & 1 \\ \end{bmatrix}^{n-1} \begin{bmatrix} a_1 \\ 1\\ \end{bmatrix} $$

$$ \begin{bmatrix} a_n \\ 1\\ \end{bmatrix}= \begin{bmatrix} -1 & 1 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 2 \\ \end{bmatrix}^{n-1} \begin{bmatrix} 0 & 1 \\ 1 & 1 \\ \end{bmatrix} \begin{bmatrix} a_1 \\ 1\\ \end{bmatrix} $$

$$ a_n= \begin{bmatrix} -1 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 2 \\ \end{bmatrix}^{n-1} \begin{bmatrix} 0 & 1 \\ 1 & 1 \\ \end{bmatrix} \begin{bmatrix} a_1 \\ 1\\ \end{bmatrix} $$

$$ a_n= \begin{bmatrix} -1 & 2^{n-1} \\ \end{bmatrix} \begin{bmatrix} 1 \\ a_1+1 \\ \end{bmatrix} $$

$$ a_n=-1+2^{n-1}(a_1+1) $$

　なおこの変形は、幾何学的に見ればアフィン変換です。

　ただこの手法、見かけはシンプルですけど計算量は多いです。対角化さえすればあとは単純ですが、そもそも対角化をするのが結構めんどうくさい。これだったらオーソドックスな特性方程式で解いた方が早いです。オシャレではあるけど実用性はないやつ。

次元を上げて行列で殴る…階差数列編

　次元を上げれば非線形な漸化式も行列計算で解決できる！　今度はさらに発展させてみましょう。

　いわゆる階差数列というやつ。

　これも漸化式を分解することによって以下のように整理できます。

$$ a_{n+1}=a_n+b_n $$

$$ b_{n+1}=b_n+1 $$

$$ \begin{bmatrix} a_{n+1} \\ b_{n+1} \\ 1 \\ \end{bmatrix}= \begin{bmatrix} 1 & 1 & 0\\ 0 & 1 & 1\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} a_n \\ b_n \\ 1 \\ \end{bmatrix} $$

$$ \begin{bmatrix} a_n \\ b_n \\ 1 \\ \end{bmatrix}= \begin{bmatrix} 1 & 1 & 0\\ 0 & 1 & 1\\ 0 & 0 & 1\\ \end{bmatrix}^{n-1} \begin{bmatrix} a_1 \\ 1 \\ 1 \\ \end{bmatrix} $$

$$ \begin{bmatrix} a_n \\ b_n \\ 1 \\ \end{bmatrix}= \begin{bmatrix} 1 & n-1 & \frac{(n-1)(n-2)}{2}\\ 0 & 1 & n-1\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} a_1 \\ 1 \\ 1 \\ \end{bmatrix} $$

$$ a_n= \begin{bmatrix} 1 & n-1 & \frac{(n-1)(n-2)}{2}\\ \end{bmatrix} \begin{bmatrix} a_1 \\ 1 \\ 1 \\ \end{bmatrix} $$

$$ a_n=a_1+(n-1)+\frac{(n-1)(n-2)}{2} $$

$$ a_n=a_1+\frac{n(n-1)}{2} $$

　このあたりになると、1次元直線における操作を3次元空間に写して計算していることになり、（この例では必要ないですが、大体の場合においては）逆行列の計算とかがエグいことになります。基本的に3次元以上の行列計算は人間のやることではないと考えています。GPUとかにやらせましょう。

補足1

　タイトルに「平面上」とありますが、正確には「のユークリッド空間上」です。タイトルのわかりやすさを優先しました。

補足2

$$ a_{n+1}=a_n+b_n $$

$$ b_{n+1}=b_n+1 $$

　を変形すると以下のような三項間漸化式（＋定数項）になります。

$$ a_{n+2} = a_{n+1}+b_{n+1} $$

$$ a_{n+2} = a_{n+1}+b_n+1 $$

$$ a_{n+2} = a_{n+1}+(a_{n+1}-a_n)+1 $$

$$ a_{n+2} = 2a_{n+1}-a_n+1 $$

　つまりこの2つの漸化式は、初期値の反映のされ方（つまり「歪み」）による見え方が違うだけで、本質的には同一のものであるといえます。実際に、得られるジョルダン標準形も同じです。

$$ \begin{bmatrix} 2 & -1 & 1\\ 1 & 0 & 0\\ 0 & 0 & 1\\ \end{bmatrix}= \begin{bmatrix} 1 & 1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 1 & 0\\ 0 & 1 & 1\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 0 & 1 & 0\\ 1 & -1 & 0\\ 0 & 0 & 1\\ \end{bmatrix} $$

　例えば、という条件を満たす初期値ベクトルは、前者では、後者ではという形になります。

*1:この図示は、私が自作したシェーダ「EigenShader」によるものです。GitHubリポジトリはここ。

アバターを高速移動させたい時に便利な、コライダーボードを用いた移動方法

！注意事項！

　以下の事項に十分に注意した上でご使用ください。

• ワールド製作者の意図しない動き（ギミックの崩壊　等）をもたらす恐れがあります。
• ワールドの舞台裏（通常ユーザーが入れない領域）を見られることが不本意な製作者もいるかも知れません。
• 演算負荷が高いので、他のユーザーのFPSを低下させる恐れがあります。

　Publicや不特定多数が集まる場、とくにギミックがあるワールドでの濫用は避けましょう。

ここから本文

　人はいつの時代も逃れたがる。仕事から、家庭から、社会から、重力から、物理法則から……。

　という訳で、バーチャル世界の中だけでも物理法則を無視して高速移動したい人向けにコライダーボード現象*1を用いたコライダーダッシュ／ジャンプのやり方を紹介します。

だいぶなめらかにコライダーダッシュ／ジャンプできるようになった pic.twitter.com/Oe9I3u2ZbX

— Hibit (@hibit_at) 2018年12月19日

　以上のような形でワールドを縦横無尽に動き回ることができます。ついでにアニメーションオーバーライドの基本的な解説もしていきます。

オブジェクトの実装

　まず高速移動させたいアバターを選択して、

「Create Empty」で空のGame Objectを作成します。

　さきほど作ったGame ObjectのComponentに「Box Collider」を追加。

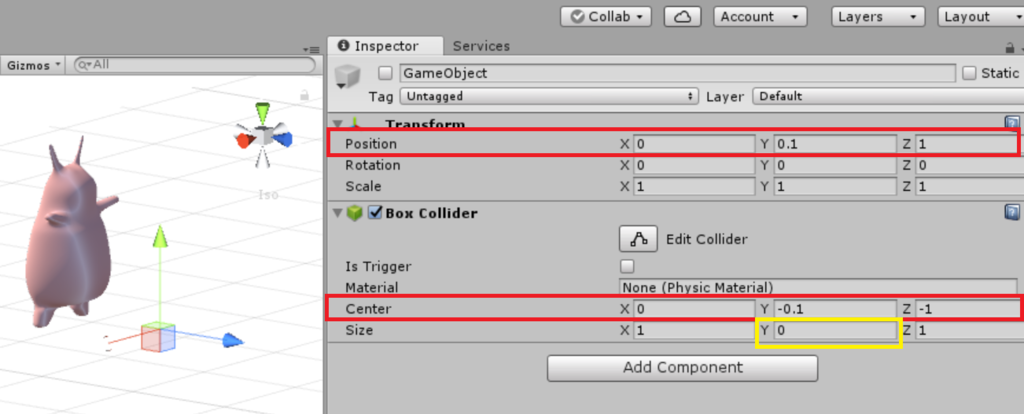
　Game Objectに以下のような設定を加えます。

• TransformのPosition…行きたい方向。
• Box ColliderのCenter…上で入力した座標と逆の座標を入力。
• Box ColliderのSize…yのサイズだけ0。

　コライダーボードは、Game Objectのコライダーとアバターのコライダーが干渉した場合、Game Objectに引き寄せられるという現象です。

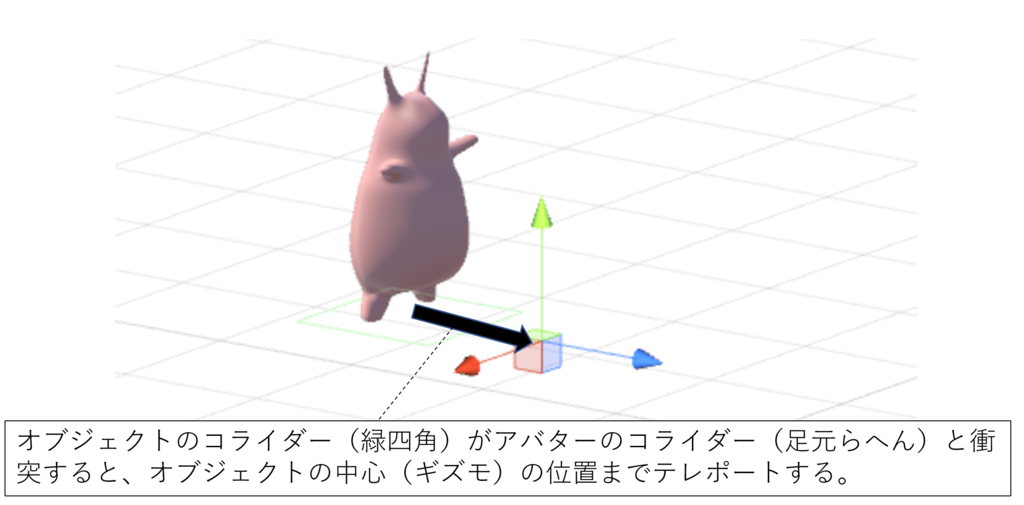
　オブジェクトのコライダーがアバターの足元にある場合、オブジェクトが存在し続ける限り「干渉→テレポート」という無限ループが繰り返されるため、結果として高速移動ができます。オブジェクトのPositionが移動方向になります。コライダーの中心は、アバターの足元に持っていくためにPositionの座標をマイナスする必要があります。

　Positionの設定としては、

• ダッシュ…
• ジャンプ…
• 空中停止…

　あたりがオススメです。ダッシュにも上方向の移動の成分を入れていますが、これについては後述します。あと、コライダーボードにはオブジェクトのRotationも反映されるため、高速回転、高速きりもみ等も再現できますが、まあ興味ある人はどうぞレベルですね。

　設定が終わったらGame Objectの脇のチェックを外して非表示にしておきましょう。これを忘れると一生高速移動し続けるアバターになり、VRChat上での操作もままならなくなります。表示／非表示で移動モードとそうでない時を切り替えられる状態にすることが必要です。次節でその手順を解説していきます。

アニメーションオーバーライドの設定

　Animationウィンドウをクリック。

「Create」ボタンをクリック。

　適当な名前で保存。画像では「dash」としていますが、別に何でもいいです。

「Add Property」でさきほど作ったオブジェクトの「Is Active」を追加。

　初期状態だと1秒（＝60フレーム＝1:00）後に設定されているキーフレームを1フレーム（0:01の位置）後まで移動した後、両フレームの「Is Active」のチェックボックスをチェックに。

　以上でアニメーションの設定は終わりですが、今度はそれをアニメータに入れていきます。

「Assets > VRCSDK > Examples > Sample Assets > Animation」の中にある「Custom Override Empty」をCtrl + ドラッグで作業フォルダにコピー。コピーした後は名前をわかりやすいものに変えておいた方が良いかもです（検索で紛らわしいので）。今回の例では「Collider Board」にしています。

　アニメータファイルを選択すると、インスペクタ欄にずらっと色々でてきますが、その中の「HANDOPEN」に先程つくったアニメーションファイル（例では「dash」）をドラッグ。なぜHANDOPENなのかは後述します。他の動作を割り当てたい場合、下の図に従って対応したアニメーションファイルを設定していきましょう。

（正確な作者は存じ上げませんが、とてもわかりやすい図。ありがたく転載させていただきます）

　今度は、アバターにアニメータファイルを設定して終わりです。

　アバターのインスペクタにある「Custom Standing Anims」にさきほど作ったアニメータファイルをドラッグ。これで、

• コントローラを操作する。
• 操作に対応したアニメーションが発動する。
• アニメーションにより、非表示だったGame Objectが表示になる。
• コライダーボード現象が起こりアバターが高速移動する。

　という機能を持つアバターが出来上がりました。

実際に動かしてみる

　アバターをVRCに上げたら、今度は実際に動かしてみましょう。あと、大事な部分を言い忘れていましたが、コライダーボード現象は床の上にいる状態だと発動しません。ジャンプするなり段差を移動するなりでなにがしか落下している状態を作り出す必要があります。

　例でHANDOPENに設定したのはこのためで、「右親指でジャンプ→他の指でグリップボタンを押す」という操作がやりやすいからです。あと、HANDOPENはグリップボタンを離すだけでアニメーションが解除されるので制御が楽というのもあります。また、ダッシュの動作に上方向の動きを入れた方がいいのもこのためで、ダッシュで高低差を稼ぐことでHANDOPEN以外の操作に割り当てたアニメーションも発動させやすくなります。

　皆様も用法用量を守ってよき高速移動ライフを（慣れない内はわりと酔います）。

*1:コライダーテレポートと呼ぶこともあります。私の場合はうれいしさん、あーあーあ～さん→SHIARUさん→私、という形で教えていただきましたが、他にも色々な方が編み出していたようです